Ask Dr. SETI ®

Mike, Virginia

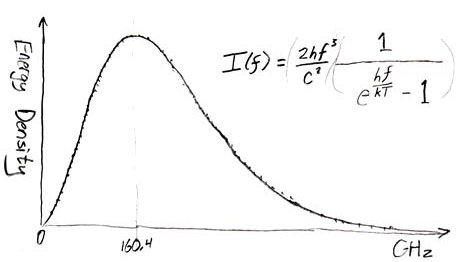
The Doctor Responds:
Yes, Mike, in fact, they can be, and are, both correct. The apparent discrepancy derives from the difference between discrete and continuous random variables, giving rise to two different definitions of "peak frequency."

The familiar Planck Curve, which shows how energy emitted by a thermal blackbody varies with frequency, appears to be a smooth curve. In fact, because energy is quantized, it is really a collection of discrete points, which only appear continuous. The independent variable depicted in a Planck Curve is not actually energy per se, but rather energy per unit of frequency, or alternatively, energy per unit of wavelength.

Since frequency and wavelength are related to each other by the speed of light, you might expect the two definitions to yield identical curves, with identical peaks. This is, however, not the case when we are talking about energy per bin. Because frequency and wavelength are inversely proportional, across the electromagnetic spectrum the respective widths of frequency bins and wavelength bins will also vary inversely one with the other.

When I previously evaluated the peak of the 2.7 Kelvin cosmic background radiation, I invoked Wien's Law. The resulting quotient of Wien's Constant over temperature produced an accurate calculation of 1.0733 mm as the wavelength at which the thermal energy per unit wavelength is at a maximum. This figure corresponds to a peak frequency of 279.5 GHz. (In fact, recent measurements from the Wilkinson Microwave Anisotropy Probe show a more precise figure of 2.715 Kelvins as the cosmic background temperature, which yields an ever so slightly different frequency of 281 GHz. For the purposes of this investigation, we can consider these two frequencies to be equal.)

However, using methodology just as sound, we can come up with an entirely different result, a frequency not at all equal to the above. Consider this alternative solution, based upon Planck's Law. One formulation of it, reproduced here, shows the distribution, as a function of temperature, of thermal energy per unit frequency:

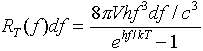
Plotting the above equation over frequency yields the familiar Planck Curve which we all know and love. Here's what it looks like:

To determine where the curve peaks, we set the derivative of the equation equal to zero, and solve for frequency. This gives us, of course, the frequency at which the slope of the curve equals zero (that is, the curve's amplitude peak). Inserting Planck's Constant, Boltzmann's Constant, and a temperature of 2.715 Kelvins, we find that this peak occurs at frequency of 160.4 GHz, the solution you cite in your question. And this solution, like my initial one, is also entirely correct. Here's an Excel Spreadsheet that will let you experiment with blackbody curves of other temperatures.

The two results differ because, in the first case, the peak being calculated is the maximum for a curve of thermal energy per unit of wavelength. In the latter computation, it is maximum thermal energy per unit of frequency we have computed.

Which is correct? They both are. Which, in the context of SETI, represents a universally recognizeable "magic frequency"? They both do.

So, which frequency should we search for alien electromagnetic artifacts? I think the answer is obvious: both.

Addendum:

David L. Wilson (PhD mathematics), a retired college professor who has also worked in thermal imaging, sends along this correction:

This has nothing to do with discrete and continuous random variables. First of all, this has nothing to do with (probability) random variables much less the difference between discrete and random ones. Rather it is entirely a result of the non-linear (inverse) function relationship between wavelength and frequency as a result derivable by calculus from that relationship. The rest of the explanation also agrees with what I just said--it contains no mention of "random variable" nor "the difference between discrete and continuous."

His full explanation appears here.